数学と芸術にみる複素数の解釈 −その2−
複素数や虚数という概念は、学校で習うような説明をされてもつまらないだけです。もっと実感の湧く、(数学や芸術が求める) 『美しさ』を持った説明ができないかと思いました。そして、それならば、逆に美術的な考えを数学の世界に当てはめたらどうだろうと思いつきました。
さて、絵については専門家ではないので (ましてプロの画家の方が見ていらっしゃるこのブログで)、絵について書くのは甚だオコガマシイのですが、絵の中の「影」についてちょっとだけ書かせてもらいます。
絵の中に描かれる影には、「実際に見えている」影と、「投げかけられる」見えない影があります。投げかけられる影とは、光が当たっている物体から、その投影された影までの空間にある、「陰」の部分です。しかし通常には、その投げかけられる影を意識することはほとんどなく、実際にその場所に入ってみなければ実感できないものです。
クロッキーという描画方法では、線で形を描写します。すべてを「線」で描く手法で、水彩画や油絵の下書きでも行われます。この時、見えている影をクロスする2方向の線で描くとすれば、投げかけられた影は、1方向の薄い線の束で描くことができます。つまり、実影と投げかけられた影は、絵の中で違う表現をされています。
このことから、投げかけられた影は、実感できないものでありながら、実影とは異なる表現をされている、絵の中で重要な「厚み」を感じさせるものと言えるのではないでしょうか。
この、実在しているかも知れないけれど意識しなければ見えない影というのは、数の世界の「虚数」と同じようなものではないかと思うのです。つまり、普段は気づくこともなく、それがなければ生活に支障が出るわけでもないのですが、それが存在することで「深み」が増し、表現をする上での「便利な道具」になるのです。
一方、もし投げかけられた影が存在しなければ、実影も存在しないのかも知れないと考えることができます。それを数の世界に当てはめると、虚数が存在しなければ実数の世界にも欠落するものが出てきてしまう。そんな風に思えてきます。
さて、数字の話に戻りましょう。現在は数の世界全体を複素数として括って表現します。そして複素数は、実数と虚数からなる数字です。例えば
3 + 5i
のように、実数部分と虚数部分の「和」として表されるのが複素数です。つまり、我々が日常の世界で目にし使っている実数は、複素数の中でも、虚数部分がゼロという特殊なものと言い換えることができます (ガウス平面上の実数を示す直線部分です)。では、虚数とは、そもそも何でしょうか?
絵の中で出てきた「投げかけられた影」には、実際にはそれがないと実影が映らないという「効果」があります。それは効果といようりも、(空間の) 性質といった方が適切かも知れません。
数の世界においても、虚数がなければ実数の世界で説明のつかない現象が起きてしまいます。例えば、次の3次方程式を見てみましょう。
x^3−15x=4
(「^」記号はべき乗を表しています。つまり「x^3」は x の三乗という意味です。)
この3次方程式の解を解くにはどうすればいいでしょうか? 実はこれ、簡単に解けるようでなかなか解けません。この式は、虚数という概念を持ち出さない限り、実数計算だけでは解を得られないことが分かっています。その細かい説明は省くとして、この3次方程式の実数解は4になります。
x=4
つまり、3次方程式自体も、その解も、実数だけでの世界にあるのに、虚数という概念を持ち出さない限りこの式は解けないのです (あてずっぽうで解くのは解法とは言えませんから)。実在する物体からその実影までの間に「投げかけられる影」の存在が不可欠なのと同様、実数の世界から実数の世界にたどり着くために、虚数の存在が欠かせないのです。ここに、実数と虚数の接点が見えます。
これを言い換えれば、数の世界は、実数と虚数が入り混じって出来ている、ということです。ちょうど、この宇宙は「時間」と「空間」とで出来ており、時間は意識しなければその存在を「感じる」ことはできないのと似ています。つまり、
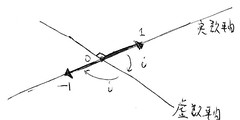
宇宙:「空間軸」+「時間軸」
数 :「実数軸」+「虚数軸」
という図式で表現でき、それぞれ空間と実数、時間と虚数が対応する存在だと考えられます。そして、「実数軸」+「虚数軸」というのは、まさに複素数そのものであり、数の世界全体を現す式だと言えるのです。
これを具体的なイメージとして捕らえるために、「数学と芸術にみる複素数の解釈 −その1−」で出てきた「ガウス平面」が役に立つのです。
ガウス平面では、整数値が並んだ点を通る実線を実数軸とし、それに直行しゼロを通る直線を「虚数軸」としています。平面上のあらゆる点は、実数と虚数の「和」として表すことができ、その和は複素数と呼ばれるわけです。
a quickr pickr post
ここで、なぜ虚数軸と実数軸が直行しているかということですが、これには訳があります。というか、ここが一番のポイントになります。
ガウス平面上では、「i を掛ける」ことを、実数軸に対して「90度回転する」と定義します。これにより、例えば実数3に i を掛けると、3i という虚数になり、虚数軸上にその点が位置することになります。もちろん、「−i を掛ける」のであれば、反対側に90度回転するということになります。
すると、「i を2回掛ける」=「i を二乗する」=「i^2」=「−1」となり、実数軸上でも、ちゃんと「−1」になることが分かります。これが、ガウス平面で虚数を表現することの利点です。要するに、虚数と実数は平面状で直行する関係にあると表現できるわけです。
さらに、平面状の任意の点は「実数部+虚数部」、つまり「a + bi」(a と b は任意の実数) と表記でき、原点ゼロからの距離として複素数の大きさを表現することになります。そうです、複素数とは、原点ゼロからの 距離 方向を持った距離だと思えばいいのです。ただ、虚数軸に沿った方向の大きさは、普段の生活の中では実感できません。だから、複素数が難しく思えてしまうのです。でもこれを単に、見えないだけで、原点ゼロからの距離だと理解すれば、何となく実感できると思います。
ところで、ガウス平面 (または複素数平面) の考え方は、その名のとおり、ヨハン・カール・フリードリヒ・ガウスという高名な数学者・物理学者・天文学者が考え出したもので、大学の数学では当たり前に出てきますが、その意味や美しさをきちんと理解している生徒はどれだけいるでしょうか。恐らく、虚数は単に「二乗すると−1になるもの」と暗記しているだけで、ガウス平面も単なる説明のための道具に過ぎないと考えているのではないでしょうか。これはとても残念なことです。もっと、その美しさを感じて欲しいものです。
複素数は数そのものであり、現実の世界を表現するもっとも自然な数といえます。それは、日常の常識がいかに部分的で小さな世界しか見ていないのかということを教えてくれるものでもあります。(先ほど説明したように、普段目にしている実数は、ガウス平面上の1つの実線部分に過ぎないのですから。)
それが証拠に、前述の例のように、虚数や複素数がなければ解けない、または記述すらできない現実の現象がこの世にはたくさん存在します。もちろん、学校で習う計算など、虚数も複素数も不要なものもたくさんありますが、それは単に、学校ではそういう簡単に解ける問題しか扱わないためです。計算練習にはなりますが、もっと現実の世界を知るための工夫も、学校では必要ではないかと思います。そこで疑問が出てきたり興味が湧いてくるのであれば、しめたものです。それが本当の意味の教育ではないかと思いますね。
少し脱線しますが、「無限」という概念についても、似たような世界観があります。無限と有限とは切っても切れないつながりがあるのです。
例えば、ある地点 A から別の地点 B までの距離を考えます。その距離をここでは「1」としましょう。単位は何でも構いません。
このとき、A から B までの距離は当然有限です。では、A から、B までの半分の地点の距離を考えて見ましょう。すると、A からそこまでの距離は「1/2」になります。しかし、これもまた有限の値です。
ところが、この中間点から A までの中間点を考えて、さらにそれをずっと繰り返していったらどうでしょうか? A から B までという有限の長さの中で、半分のその半分、そのまた半分という地点は、無限に得られます。つまり、(概念上は) 有限の長さに無限が潜んでいるということになります。(現実には、量子力学で扱える最小の単位はプランク長なので、それよりも短い距離を扱うことは無理ですが。。。)
これは有名な哲学上の話なのですが、実世界が「有限」+「無限」という座標軸で現すことができるとうことを示すものです。そう、まさに、宇宙が「空間軸」+「時間軸」で、数が「実数軸」+「虚数軸」で現せること、そして絵には「投げかけられた影」と「実影」があることに似ています。これも、人間の常識や認識可能な事象が、いかにいい加減なものであるかを示すと同時に、魅力的で美しい世界観を見せてくれるものです。
さて、数の歴史から虚数の捕らえ方についていろいろ書いてきましたが、学校で習う虚数や複素数の定義から得られたイメージよりは、その美しさや意義、有用性、そして必然性が何となく見えてきたのではないでしょうか。数学を専門に勉強している方から見れば幼稚な説明かも知れませんが、あまり数学と関わったことがない、または関わりたくなかった人にとって、興味を持つきっかけになってもらえれば幸いです。